The Black-Scholes Model: A Practical Guide for Options Traders

The Black-Scholes Model is one of the most widely used tools in options pricing, helping traders estimate the fair value of options contracts. But for many, its complex formula can feel intimidating. In this guide, we’ll break down the Black-Scholes Model into easy-to-understand terms, focusing on how you can use it in real-world trading.

Whether you’re trading stock options, forex, or other assets, the Black-Scholes Model can help you make better decisions. We’ll show you how to apply this model practically and how to use it alongside other tools for better trading outcomes.

What is the Black-Scholes Model?

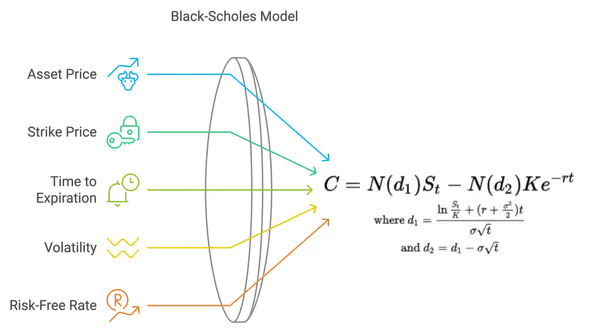
At its core, the Black-Scholes Model is a mathematical model that calculates the fair price of an option based on five key factors: the current price of the asset, the strike price of the option, the time to expiration, the risk-free interest rate, and the volatility of the asset.

Key Components of the Black-Scholes Formula

Asset Price: The current market price of the asset.
Strike Price: The predetermined price at which the option can be exercised.
Time to Expiration: The amount of time remaining until the option’s expiration date.
Volatility: The expected fluctuation of the asset’s price.
Risk-Free Rate: The theoretical return on a risk-free investment, typically the yield on government bonds.
By plugging these inputs into the Black-Scholes formula, you can calculate the option’s theoretical price. But let’s break it down further into how traders can use it in a more practical context.

The Founders Behind the Model

Fischer Black and Myron Scholes were both experts in the field of finance and known for their pioneering work in options pricing. Together with Robert Merton, who contributed to the model’s development, they were awarded the Nobel Prize in Economic Sciences in 1997.

Black, a former MIT professor, and Scholes, a renowned economist, collaborated to create a groundbreaking model that revolutionized the way financial derivatives are priced. Their innovative approach to quantifying risk and return paved the way for modern financial engineering.

The Primary Purpose of the Model

The Black-Scholes Model provides a theoretical framework for valuing options based on certain assumptions. By determining the fair price of an option, it helps investors make informed decisions about buying or selling options. It also plays a crucial role in risk management strategies.

Furthermore, the model’s impact extends beyond the realm of options pricing. Traders and analysts apply its concepts to various areas of finance, including calculating implied volatility and developing other derivative pricing models. The Black-Scholes Model stands as a testament to the power of mathematical modeling in understanding and navigating the complexities of financial markets.

How the Black-Scholes Model Helps in Real Trading

While the formula itself can seem daunting, understanding what it does is relatively simple: it helps you determine whether an option is overpriced or underpriced compared to the market. By comparing the Black-Scholes price with the actual market price of the option, you can make better-informed decisions about whether to buy or sell.

Imagine you’re looking at a call option on a stock currently priced at $100, with a strike price of $105, expiring in one month. You expect the stock’s volatility to be around 20%, and the current risk-free rate is 1%. By using the Black-Scholes Model, you calculate that the fair price for this option should be $2.50. If the market is pricing the option at $3.00, you might consider it slightly overvalued, giving you insight into your decision-making.

How to Use the Black-Scholes Model: Step-by-Step Guide

Here’s how you can start applying the Black-Scholes Model in your trading strategy:

1. Gather the Data: You’ll need the current asset price, the strike price, time to expiration, volatility, and the risk-free rate. Most trading platforms and financial websites will provide these values.

2. Use a Black-Scholes Calculator: Luckily, you don’t need to solve the equation by hand. There are many free Black-Scholes calculators available online that can do the heavy lifting for you. Simply input the values to calculate the option price.

3. Compare with Market Price: Once you have the Black-Scholes price, compare it with the actual market price of the option. Is the option overvalued or undervalued?

4. Make Your Trade: Use this information alongside other indicators and your market analysis to decide whether to buy, sell, or hold your option position.

Example:

Let’s say the Black-Scholes Model prices a put option at $1.50, but the market price is $2.00. This could indicate that the market is expecting higher volatility than what you’ve calculated, providing an opportunity for you to analyze further and adjust your strategy.

The Fundamental Assumptions of the Black-Scholes Model

The Black-Scholes Model, a groundbreaking formula in the world of finance, is built upon several key assumptions that are crucial for its accuracy and usefulness. Let’s delve deeper into each of these assumptions to understand their significance in the context of options pricing.

Assumption of Risk-Neutral Investors

One of the cornerstones of the Black-Scholes Model is the assumption that investors are risk-neutral. This assumption implies that investors are indifferent to risk and solely focused on maximizing their expected returns. While in reality, investors exhibit varying degrees of risk aversion, assuming risk neutrality simplifies the calculations by allowing the use of risk-free interest rates. This simplification is essential for the model’s applicability in pricing options and other derivatives accurately.

Assumption of Constant Volatility

Another critical assumption of the Black-Scholes Model is the constancy of volatility in the underlying asset’s price. Volatility, a measure of the asset’s price fluctuations, is assumed to remain constant over the option’s lifespan. This assumption, although not always reflective of market dynamics, aids in predicting future price movements and calculating expected returns. By assuming constant volatility, the model streamlines the valuation process, providing a more straightforward framework for pricing options.

Assumption of No Dividends

Furthermore, the Black-Scholes Model operates under the assumption that the underlying asset does not issue any dividends during the option’s existence. While this assumption may not align with real-world scenarios where dividends play a significant role in investment decisions, it serves a crucial purpose in simplifying the valuation methodology. By disregarding dividend payments, the model focuses on the core elements of option pricing, allowing for a more efficient and standardized approach to valuation.

The Mathematical Framework of the Black-Scholes Model

At the heart of the Black-Scholes Model is a partial differential equation known as the Black-Scholes equation. This equation relates the price of a derivative security to the price of the underlying asset, time, and other variables.

Understanding the Black-Scholes Equation

The Black-Scholes equation is a continuous-time model that helps in calculating the fair price of options. It takes into account factors such as the current price of the underlying asset, the time to expiration, the risk-free interest rate, and the volatility of the underlying asset.

This equation is derived from the principle of risk-neutral pricing, which assumes that investors are indifferent to risk and will require a risk-free rate of return to hold a risky asset. By incorporating these variables into the equation, the Black-Scholes Model provides a mathematical framework for determining the theoretical price of options under certain assumptions.

The Role of the Normal Distribution

A key concept in the Black-Scholes Model is the assumption that the price movements of the underlying asset follow a log-normal distribution. This assumption allows for the application of statistical techniques based on the normal distribution, making the model more accurate and reliable.

By assuming that asset prices follow a log-normal distribution, the Black-Scholes Model accounts for the skewness and kurtosis observed in financial markets. This statistical foundation enables traders and analysts to make informed decisions about option pricing and risk management, enhancing the efficiency and effectiveness of financial markets.

Limitations of the Black-Scholes Model

While the Black-Scholes Model is widely used, it’s important to recognize its limitations:

1. Assumption of Constant Volatility: The model assumes that volatility remains constant over time, which isn’t always true in real markets.

2. No Accounting for Dividends: If you’re trading options on dividend-paying stocks, the Black-Scholes Model doesn’t factor in dividends unless adjusted for them.

3. Assumption of European Options: Assumption of European Options: The model treats options as exercisable only at expiration, making it ideal for European-style options. Traders need to make slight adjustments for American options, which allow exercise at any time.”

Black-Scholes Model vs. Other Option Pricing Models

It’s helpful to compare the Black-Scholes Model with other options pricing models, such as the Binomial Model, to understand when it may be more or less suitable.

• Black-Scholes Model: Best for European-style options and provides a quick, simplified approach.
• Binomial Model: Offers more flexibility and can better handle American-style options and changing volatility.

FAQ

What is the Black-Scholes Model?

The Black-Scholes Model is a mathematical formula used to calculate the fair price of options. It takes into account factors such as the current price of the underlying asset, time to expiration, risk-free interest rate, and volatility.

Who developed the Black-Scholes Model?

Economists Fischer Black and Myron Scholes developed the Black-Scholes Model, with contributions from Robert Merton. Their work earned them the Nobel Prize in Economic Sciences in 1997.

What are the assumptions of the Black-Scholes Model?

The Black-Scholes Model assumes risk-neutral investors, constant volatility, and no dividends paid by the underlying asset during the option’s lifespan.

What are the key variables in the Black-Scholes Model?

The key variables in the Black-Scholes Model are the stock price and strike price, time to expiration, risk-free interest rate, and volatility. These variables play a significant role in determining the value of options.

With a solid understanding of the Black-Scholes Model, you are now equipped to navigate the world of options trading with confidence. Remember to consider the model’s limitations and supplement your analysis with other factors for a comprehensive approach to trading. Happy investing!

With your new understanding of the Black-Scholes Model, elevate your options trading to the next level using Morpher. Experience the future of investing on a platform that offers zero fees, infinite liquidity, and the ability to trade a vast array of assets, from stocks to NFTs. With Morpher, you can start investing with just $1, enjoy up to 10x leverage, and trade with confidence knowing you have full control over your funds. Ready to transform your trading experience? Sign Up and Get Your Free Sign Up Bonus today and join the revolution at Morpher.com.

Disclaimer: All investments involve risk, and the past performance of a security, industry, sector, market, financial product, trading strategy, or individual’s trading does not guarantee future results or returns. Investors are fully responsible for any investment decisions they make. Such decisions should be based solely on an evaluation of their financial circumstances, investment objectives, risk tolerance, and liquidity needs. This post does not constitute investment advice.